|
|
Download Free & Fully Functional Product Trials | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
All Downloads |
Nevron Map for SharePoint supports an unlimited number of map layers. Each map layer can display either a predefined or custom ESRI map.
The report item comes with the following built-in maps:
Each map layer can have its own settings for fill rule, display on legends and dynamic shape appearance and action.
When making choropleth maps, you are often required to fill the map using a filling rule that splits the input dataset into a user-defined number of ranges.
Nevron Map for SharePoint supports two- and three-color filling rules with a user-specified number of ranges.
The dataset is automatically split into the specified ranges according to one of the following distribution rules:
To see geographical data on a 2D device such as a monitor or printer, that data must be projected to a 2D plane using a map project that transforms longitude/latitude coordinates into 2D coordinates.
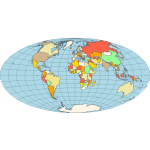 Aitoff- Proposed by David A. Aitoff in 1889, it is the equatorial form of the azimuthal equidistant projection but stretched into a 2:1 ellipse while halving the longitude from the central meridian. 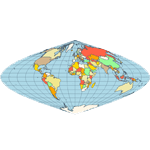 Bonne- a pseudoconical equal-area map projection. All parallels are standard, with the same scale as the central meridian; parallels are concentric circles — no distortion along the reference parallel or the central meridian. Cylindrical Equal-Area - represents a cylindrical equal-area projection of the Earth. The following is a summary of cylindrical equal-area projection's special cases:
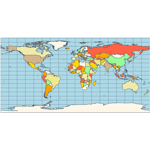 Equirectangular - a projection that maps meridians to equally spaced vertical straight lines and parallels to equally spaced horizontal straight lines. 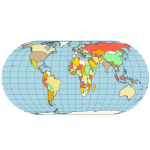 Eckert IV - pseudocylindrical and equal-area projection. The central meridian is straight, the 180th meridians are semi-circles, and other meridians are elliptical. Scale is true along the parallel at 40:30 North and South. 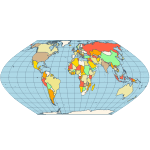 Eckert VI - pseudocylindrical and equal-area projection. The central meridian and all parallels are at right angles. All other meridians are sinusoidal curves. Shape distortion increases at the poles. Scale is correct at standard parallels of 49:16 North and South. 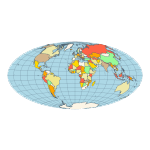 Hammer- an equal-area map projection, described by Ernst Hammer in 1892. Directly inspired by the Aitoff projection, Hammer suggested the use of the equatorial form of the Lambert azimuthal equal-area projection instead of Aitoff's use of the azimuthal equidistant projection. Visually, the Aitoff and Hammer projections are very similar, but Hammer has seen more use because of its equal-area property. 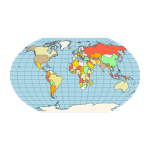 Kavrayskiy VII -a map projection invented by V. V. Kavrayskiy in 1939 for a general-purpose pseudocylindrical projection. Like the Robinson projection, it is a compromise intended to produce good quality maps with low distortion overall. Despite straight, evenly-spaced parallels and a simple formulation, it scores well compared to other popular projections, such as the Winkel Tripel. It has been used in the former Soviet Union but is almost unknown in the Western world. 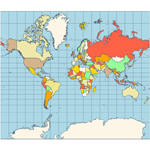 Mercator- introduced in 1569 by Gerardus Mercator. It is often described as a cylindrical projection, but it must be derived mathematically. The meridians are equally spaced, parallel vertical lines, and the parallels of latitude are parallel, horizontal straight lines, spaced farther and farther apart as their distance from the Equator increases. This projection is widely used for navigation charts because any straight line on a Mercator-projection map is a line of constant true bearing that enables a navigator to plot a straight-line course. It is less practical for world maps because the scale is distorted; areas farther away from the equator appear disproportionately large. On a Mercator projection, for example, the landmass of Greenland appears to be greater than that of the continent of South America; in the actual area, Greenland is smaller than the Arabian Peninsula. 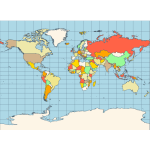 Miller Cylindrical - a modified Mercator projection proposed by Osborn Maitland Miller (1897-1979) in 1942. The parallels of latitude are scaled by a factor of 0.8, projected according to Mercator, and then the result is divided by 0.8 to retain scale along the equator. 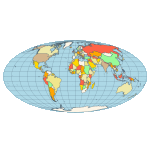 Mollweide- The Mollweide projection is a pseudocylindrical map projection generally used for global maps of the world (or sky). Also known as the Babinet projection, homolographic projection, or elliptical projection. As its more explicit name Mollweide equal-area projection, indicates, it sacrifices fidelity to angle and shape in favor of an accurate depiction of the area. It is used primarily where accurate representation of area takes precedence over shape, for instance, small maps depicting global distributions. 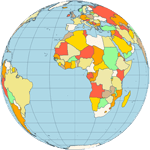 Orthographic- a perspective (or azimuthal) projection in which the sphere is projected onto a tangent plane. It depicts a hemisphere of the globe as it appears from outer space. The shapes and areas are distorted near the edges, but distances are preserved along parallels. 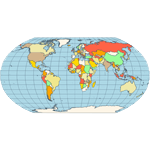 Robinson- made in 1988 to show the entire world at once. It was specifically created in an attempt to find a good compromise to the problem of readily showing the whole globe as a flat image. The projection is neither equal-area nor conformal, abandoning both for a compromise. The creator felt this produced a better overall view than could be achieved by adhering to either. The meridians curve gently, avoiding extremes, stretching the poles into long lines instead of leaving them as points. Hence distortion close to the poles is severe but quickly declines to moderate levels moving away from them. The straight parallels imply severe angular distortion at the high latitudes toward the outer edges of the map, a fault inherent in any pseudocylindrical projection. 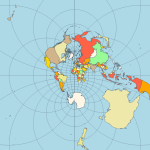 Stereographic- it is a particular mapping (function) that projects a sphere onto a plane. No map from the sphere to the plane can accurately represent both angles (and thus shapes), and areas are cartography's fundamental problem. Area-preserving map projections are generally preferred for statistical applications because they behave well for integration, while angle-preserving (conformal) map projections are preferred for navigation. The stereographic projection falls into the second category. 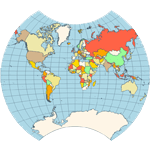 Van der Grinten- neither equal-area nor conformal projection. It projects the entire Earth into a circle, though the polar regions are subject to extreme distortion. The projection offers a pleasant balance of shape and scale distortion. The boundary is a circle; all parallels and meridians are circular arcs (spacing of parallels is arbitrary)—no distortion along the standard parallel at the equator. 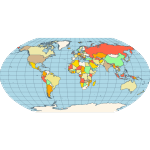 Wagner VI -a pseudocylindrical whole Earth map projection. Like the Robinson projection, it is a compromise projection with no special attributes other than a pleasing, low distortion appearance. 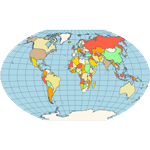 Winkel Tripel- a modified azimuthal map projection proposed by Oswald Winkel in 1921. The projection is the arithmetic mean of the equirectangular projection and the Aitoff projection. Goldberg & Gott shows that the Winkel Tripel is arguably the best overall whole-earth map projection known, producing minimal distance errors, small combinations of ellipticity and area errors, and the smallest skewness of any map. In 1998, the Winkel Tripel projection replaced the Robinson projection as the standard projection for world maps made by the National Geographic Society.
Nevron Map for SharePoint features full control over the map parallels and meridians visibility, appearance, and step.
You can display parallels and meridians with fine, normal, or coarse density.
Parallels and meridians can be displayed behind or above the map.
Nevron Map for SharePoint allows you to control the displayed geographical bounds in several ways:
Nevron Map for SharePoint can also be centered in several ways:
Following is a brief list of some of the most important additional customization options that the map designer visually exposes:
|
We use cookies to allow us to automate the access and the data entry functions of our website and to correlate online ordering information for purchases you may make while at the website (if any), tailor our website to your preferences or interests, or customize promotions or marketing. For full details read our cookie policy.