ProductsAll Products
.NET Components
DownloadsAll Downloads
Nevron Chart for .NET supports four types of surface charts that differ in how data is passed to the control. Those are the grid surface, mesh surface, triangulated surface, and vertex surface chart types. They all share common functionality regarding the displayed filling, contour lines, and support for hit testing. All surface charts support rendering with or without GPU acceleration on various platforms such as WPF, WinForms, and ASP.NET.
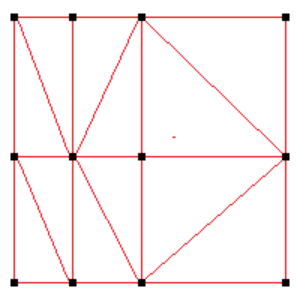
Let’s first look at how data is organized with each of those surface charts starting with the grid surface. In this surface chart, data is organized in a regularly or irregularly spaced grid along the X/Y plane, where all points that lie on the same row or column share the same y and x coordinate, respectively. The picture on Fig.1 shows how the control will split the data in an irregular grid surface series into distinct triangles::
Note that the control can choose between connecting the top left and bottom right vertex or the top right and bottom left vertex. This is configurable, and you have options to force the control always to pick one or the other diagonal or choose based on the elevation of the vertexes.
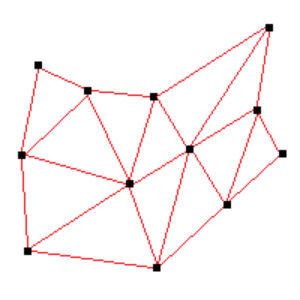
Similarly, a mesh surface series is also represented by a grid of three-dimensional points, the difference being that each point can have different X/Y coordinates, as illustrated in Fig.2.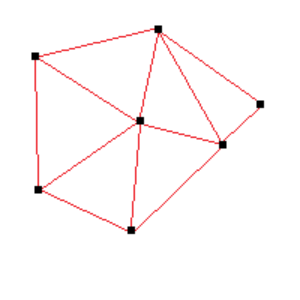
The mesh can also pick between the left top / right bottom and right top / left bottom, like the grid surface series.
Next, there is the triangulated surface series. The input data for this surface series can be an arbitrary set of points in 3D. The control will create a Delaunay triangular mesh based on this set. For example:
The image from Fig.3 shows how the triangulated mesh looks when looked at from the top. The Delaunay triangulation is characterized by each set of arbitrary 3D points having only one Delaunay triangulation. Further, this triangulation guarantees that the produced triangles are maximally equilateral and non-interesting
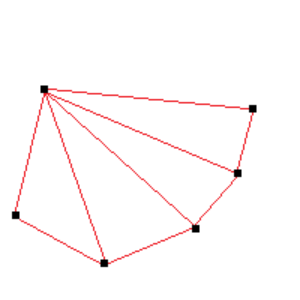
Finally, there is the vertex surface series which accepts a set of points and a vertex primitive. For example, the following image illustrates a vertex surface series with six points and a triangle fan vertex primitive. The triangle fan center point is located at the top left corner of the image:
After we’ve covered the basics, let’s look at some C# code showing how to display the standard normal distribution function along the x/y plane as a 3D surface chart. In its most simple form, the code will look like this:
// configure chart to display 3D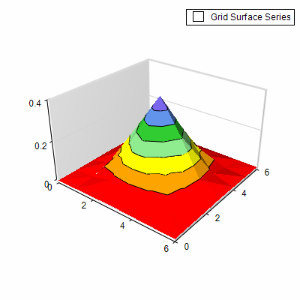
This code will produce the following surface:
Suppose that you want to change the color palette associated with the surface to something different – for example, shades of red to green that map blue to zero values and red to 0.5 – the code to do this is:
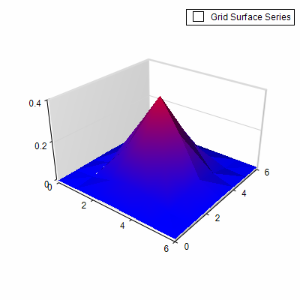
Suppose that you want to change the color palette associated with the surface to something different – for example, shades of red to green that map blue to zero values and red to 0.5 – the code to do this is:
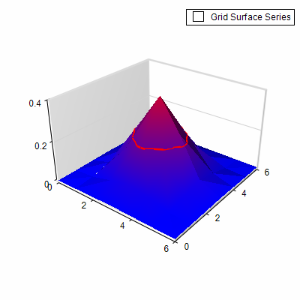
Next, suppose we want to mark the value of 0.2 on this surface. For this purpose, we can use an isoline:
surfaceSeries.Isolines.Add(new NSurfaceIsoline(0.2, new NStrokeStyle(2, Color.Red)));
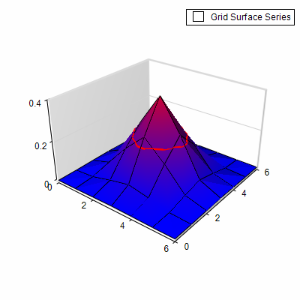
And display the triangle mesh:
surfaceSeries.FrameMode = SurfaceFrameMode.Mesh;